CLASS1:TUESDAY 08/09/2020
SOLUTION TO ASSIGNMENT
The floor of a rectangular room is 5.22m by 3.91m.The room is 2.76m high. Round the given data to the nearest whole meter and hence estimate:
- The area of the floor in m2
- The volume of the room in m3
SOLUTION
The area of the floor is given as
length*width
where length=5.22m and width=3.91m
5.22*3.9=20.355m2
The volume of the room in m3
The volume is given as
length*width*height=
5.22*3.9*2.76
56.18808m3
QUESTION2
A circular room has a floor of diameter 590cm.Estimate:
a)The perimeter of the room in meters
SOLUTION
Perimeter of a circular object is given as pi*diameter
Π*d
Where π=3.142 and d=590cm
3.142*590
=1853.78cm
b)The area of the floor in m2
this is given as
πr2 where r=d/2=590/2=295
3.142*295*295
273432.55m2
CLASS2:WEDNESDAY 09/09/2020
QUESTION1
1)A car is approximately 4.5m long and 1.7m wide. At the factory where they were made the cars are packed as closely as possible in a rectangular parking area 200m by 150m.Estimate the total number of cars that can be stored in the area.
Area of the car=
Length*width=
4.5m*1.7m
7.65m2
Area of the room=
200m*150m
30000m2
Total number of cars that can stored=30000/7.65
3921.57
Approximately 4000 cars
QUESTION2
2)A cylindrical wooden column is 3m high and 28cm in diameter. Uses the value of 3 for pi calculate:
)The volume of column
b) b)The mass, in kg of the column if the density of the wood is 0.8g/cm3
The volume of the column is given as
Πr2h
Where h=3m and radius=28/2=14cm
3*142*3
1764m3
b)The mass, in kg of the column if the density of the wood is 0.8g/cm3
Density=mass/volume
Density=0.8g/cm3 and volume=1764cm3
Mass=density*volume
=0.8*1764=1411.2g
CLASS 1: TUESDAY 01/09/2020
The floor of a rectangular room is 5.22m by 3.91m.The room is 2.76m high. Round the given data to the nearest whole meter and hence estimate:
- The area of the floor in m2
- The volume of the room in m3
2)A circular room has a floor of diameter 590cm.Estimate:
a)The perimeter of the room in meters
b)The area of the floor in m2
3)A car is approximately 4.5m long and 1.7m wide. At the factory where they were made the cars are packed as closely as possible in a rectangular parking area 200m by 150m.Estimate the total number of cars that can be stored in the area.
CLASS2:Wednesday 02/09/2020
1)Calculate the area of a sector of a circle of radius 12cm and angle 1500
2)A cylindrical wooden column is 3m high and 28cm in diameter. Uses the value of 3 for pi calculate:
a)The volume of column
b)The mass, in kg of the column if the density of the wood is 0.8g/cm3
CLASS3: THURSDAY 03/09/2020
1) Calculate the curved surface area of cylinder of radius 6cm and height 15cm.
2) Calculate the area of a sector of a circle of radius 21cm and angle 3000
3)A plastic cylinder is in the shape of an open cylinder.Ih has a lid of an open cylinder with height 2cm and diameter 8.2cm.The base has diameter of 8cm and height 10cm. Use the value of 3.1 for pi to find:
a) The surface area of the container
b)The surface area of the lid.
CLASS1:TUESDAY 25/08/2020
1)Calculate the total surface area of a solid cone of slant height 10cm and base diameter 10cm.Use the value of 3.14 for π .
2)Calculate the total surface area of a solid cone of vertical height24cm and base diameter .
3)Calculate the total surface area of a solid cone of base radius 6cm and slant height of 10cm.
CLASS2 :WEDNESDAY 26/08/2020
(Use value of 3.14 for π)
1)Calculate the total surface area of a solid cone of base radius 8cm and vertical height 6cm.
2)Calculate the total surface area of a solid cone of vertical height 12cm and base radius 5cm.
3) Calculate the total surface area of a solid cone of slant height 25cm and vertical height 24cm.
CLASS3: THURSDAY 27/08/2020
1)A mound of beans is roughly in the shape of a cone of height 20cm and base radius 30cm. Use the value of 3 for π to find the approximate volume of beans.
2) A cone and cylinder have equal volumes and bases of the same diameter .If the height of the cone is 27cm, what is the height of the cylinder?
3)Calculate the volumes of cones with height 6cm, base radius of 7cm.
CLASS1:TUESDAY 18/08/2020
1)Calculate the volume of cylindrical bar 32cmcm long and 5.4cm in diameter(Take π to be 22/7)
2)Calculate the total surface are area of a cylinder with radius 8cm and diameter of 21cm(Take π to be 22/7)
3)Calculate the volume of a cylinder of height of 22cm and radius 84cm (Take π to be 22/7)
Class2:Wednesday 19/08/2020
- 102litres of oil are poured into a cm cylindrical drum 100cm in diameter .How deep is the oil in the drum.
- Around brass is 10m long and 128mm in radius.
How many liters of water will a cylindrical pipe hold if it is 8m long and 7cm in diameter? (Take π to be 3.142)
- A cylindrical tank is 24m in diameter and 14m deep. How many kilolitres will it hold?
CLASS3:THURSDAY 20/08/2020
1)A mound of beans is roughly in the shape of a cone of height 20cm and base diameter of 60cm.Use the value of 3 for π to find the approximate volume of beans.
2)A cone and a cylinder have equal volumes and base of the same diameter .If the height of the cone is 27cm, what is the height of the cylinder?
3)Use the value of 22/7 for π to calculate the volume of cone with height 6cm, base radius 7cm.
CLASS 1:TUESDAY 11/08/2020
QUESTION1
Calculate the volume of cylindrical bar 8cm long and 3.5cm in diameter
Solution
The volume of a cylinder is given by π r2h
Where r=3.5/2 =1.75 and h=8cm
This equals π 1.752*8
22/7*1.75*1.75*8
This equals to
77cm3
QUESTIONS 2
99l of oil are poured into a cm cylindrical drum 60cm in diameter .How deep is the oil in the drum.
SOLUTION
99liters= 99*1000 cm3= 99000cm3
The volume of a cylinder is given by π r2h
Where r=60/2 =30cm h=?
99000= π*302*h
99000= π900*h
This gives us
99000/ (π*900)=h
Therefore
h=110/ π
h=110/22/7
h=110*7/22
h=35cm
QUESTION 3
3) A wooden roller is 1m long and 8cm in diameter .Find its volume in cm3
SOLUTION
The volume of a cylinder is given by π r2h
Where r=8/2 =4cm h=1m=100cm
Volume then equals
π *4*4*100=
π*16*100
1600 π
1600*22/7
Which equals to
5028.57cm3
CLASS 2 :WEDNESDAY 12/08/2020
QUESTION 1
- Around brass is 5m long and 14mm in radius.
SOLUTION
The volume of a cylinder is given by π r2h
Where h=5m which is 5000mm
Radius=14mm
Π*142*5000
Π*980000
22/7*980000
3080000mm2
QUESTION 2
SOLUTION
2) Four cylindrical concrete pillars support the roofs of a building .Each pillar is 4m long and 50cm in diameter.
The volume of a cylinder is given by π r2h
Where h=4m =400cm and diameter=50m radius=50/2=25cm
π *25*25*4
this equals
(22/7)*625*4
7857.14cm3
4 of such pillars is
4*7857.14
31428.57cm3
QUESTION 3
3)How many liters of water will a cylindrical pipe hold if it is 1m long and 7cm in diameter?
SOLUTION
The volume of a cylinder is given by π r2h
Where h=1m=100cm ,diameter=7cm radius=7/2=3.5cm
Π*3.52*100
22/7*3.5*3.5*100 3850cm3
CLASS 3 :THURSDAY 13/08/2020
QUESTION1
1)A cylindrical container has a diameter has diameter of 14cm and height of 20cm and is full of water .A student pours the water into another cylinder of diameter 20cm.How deep is the water in the second cylinder.
SOLUTION
The volume of a cylinder is given by π r2h
Where h=20cm and diameter=14 cm radius=14/2=7cm
Π*72*20
This is equals to
(22/7)*7*7*20
This is
22*7*20
3080cm3
The volume is emptied into another container of diameter 20cm
The radius is 20/2=10cm
3080= π*102*h
Therefore
h=3080/( π*100)
h=9.8026cm
QUESTION2
SOLUTION
2) A cylindrical storage vessel is 4m in diameter and 31/2m deep. How many kilolitres will it hold?
The volume of a cylinder is given by π r2h
Where h=7/2cm and diameter=4cm radius= 4/2=2cm
Π*22*7/2
Π*4*7/2
This equals
(22/7 )*4*7/2
22*4/2
44cm3
CLASS1: TUESDAY 04/08/2020
Use the value of 22/7 for pi
1) Calculate the volume of a cylindrical steel bar which is 8cm long and 3.5cm in diameter
2)99l of oil are poured into a cmcylindrical drum 60cm in diameter .How deep is the oil in the drum.
3) A wooden roller is 1m long and 8cm in diameter .Find its volume in cm3
CLASS2: WEDNESDAY 05/08/2020
- Around brass is 5m long and 14mm in radius.
a)Calculate its volume in cm3
b) if the density of the brass is 8g/cm3 , calculate the mass of the bar in kg.
2)Four cylindrical concrete pillars support the roofs of a building .Each pillar is 4m long and 50cm in diameter
a)Calculate the total volume of the four pillars in m3
b)If 1 m3 of concrete has a mass of 2.1 tons, calculate the total mass of the four pillars in tons
3)How many liters of water will a cylindrical pipe hold if it is 1m long and 7cm in diameter?
CLASS 3:THURSDAY 06/08/2020
1)A cylindrical container has a diameter has diameter of 14cm and height of 20cm and is full of water .A student pours the water into another cylinder of diameter 20cm.How deep is the water in the second cylinder.
2)A cylindrical water tank is70cm in diameter .To begin with it is full of water. A leak starts in the bottom so that it loses 10l of water every hour. How long will it take for the water level to fall by 20cm.
3) A cylindrical storage vessel is 4m in diameter and 31/2m deep. How many kilolitres will it hold?
CLASS 1:TUESDAY 28/07/2020
1)Calculate the volume of a cylinder of radius 8.1cm and height 7.6cm(take pi to be 3.142)
2)Calculate the volume of a cylinder of radius 25cm and height 21cm(take pi to be 22/7)
3)Calculate the volume of a cylinder of radius 35cm and height of 42cm(take pi to be 22/7)
CLASS 2 :WEDNESDAY 29/07/2020
1)A closed tin is in the shape of a cylinder of diameter 10cm and height 15cm.Use the value 3.14 for pi to find:
a)the total surface area of the tin
b) the value of the tin to the nearest naira if tin plate costs 600 naira per m3
2)Calculate the volume of a cylinder of diameter 14cm and height 10cm(take pi to be 22/7)
3)Calculate the volume the cylinder of height 21cm and radius 56cm(take pi to be 22/7)
CLASS3 :THURSDAY 30/07/2020
1)62 Liters of water are poured into a cylinder of diameter 40cm. Use the value 3.1 for pi to find how deep the water is in the cylinder
2) Estimate the capacity in liters of a cylindrical drum which is 45cm in diameter and 66cm high(take pi to be 3.14)
3)Take pi to be 3.1 and calculate the volume of a cylinder of height 10cm and radius 4cm
CLASS1:TUESDAY 28/07/2020
1)Calculate the volume of a cylinder of radius 8.1cm and height 7.6cm(take pi to be 3.142)
2)Calculate the volume of a cylinder of radius 25cm and height 21cm(take pi to be 22/7)
3)Calculate the volume of a cylinder of radius 35cm and height of 42cm(take pi to be 22/7)
CLASS 2:WEDNESDAY 29/07/2020
1)A closed tin is in the shape of a cylinder of diameter 10cm and height 15cm.Use the value 3.14 for pi to find:
a)the total surface area of the tin
b) the value of the tin to the nearest naira if tin plate costs 600 naira per m3
2)Calculate the volume of a cylinder of diameter 14cm and height 10cm(take pi to be 22/7)
3)Calculate the volume the cylinder of height 21cm and radius 56cm(take pi to be 22/7)
CLASS3:THURSDAY 30/07/2020
1)62 Liters of water are poured into a cylinder of diameter 40cm. Use the value 3.1 for pi to find how deep the water is in the cylinder
2) Estimate the capacity in liters of a cylindrical drum which is 45cm in diameter and 66cm high(take pi to be 3.14)
3)Take pi to be 3.1 and calculate the volume of a cylinder of height 10cm and radius 4cm
CLASS1:TUESDAY 21/07/2020
CORRECTION
QUESTION1
Calculate the curved surface area of a cylindrical container with these
dimensions:
(Take π=3.142)
Diameter 20cm, length 32cm
SOLUTION
The curved surface area of a cylinder is given by 2πrh
Where r=diameter/2 =20/2=10cm Length= height=32cm
The curved surface area is 2*3.142*10*32
Which is equal to 2010.88cm2?
QUESTION 2
Calculate the curved surface area of a cylindrical container with these
dimensions:
(Take π=3.142)
Diameter 52cm, height 42cm
Solution
The curved surface area of a cylinder is given by 2πrh
Where r=diameter/2 =52/2=26cm Length= height=42cm
The curved surface area is 2*3.142*26*42
Which is 6862.128cm2
QUESTION3
Take π to be 22/7 to find the total surface area of a closed cylinder of radius 7cm and height 30cm.
SOLUTION
Total surface area of a closed cylinder is given as
2πr2+2πrh
This can be simplified as
2πr(r+h)
Where r=7cm, h=30cm and π=22/7
This equals to
2π*7(7+30)
14*π(37)
14*22/7(37)
This is simplified as
2*22*37
This equals
1628cm2
CLASS2 :WEDNESDAY 22/07/2020
QUESTION1
1)A closed tin is in the shape of a cylinder of diameter 42cm and height
300cm.Use the value of 22/7 for π to find the curved surface area of the tin
SOLUTION
The curved surface area of a cylinder is given by 2πrh
Where r=diameter/2 =42/2=21cm , height=300cm
The curved surface area is 2*3.142*21*300
This equals to
39589.2cm2
QUESTION 2
A cylindrical cup has a circular base of radius 35 cm and height
of 20cm.Taking the value of π to be 22/7 calculate:
a) Total surface area
b) the area of its circular base
SOLUTION
Total surface area of a cylindrical cup is given as
πr2+2πrh
r=35cm, h=20cm and π=22/7
22/7*35*35 +2*22/7*35*20
22*5*35 +22*5*20
3850+2200
6050cm2
b)Area of its circular base is given as
Area of circular base is given as
Πr2
Where r=35cm
This equals to
22/7*35
This is simplified as
22*5
110cm2
QUESTION3
A closed cylinder is of height 30cm and base radius 6cm.Use the value 3.14 for π to
calculate the total surface to the nearest cm2
Total surface area of a closed cylinder is given as
2πr2+2πrh
This can be simplified as
2πr(r+h)
Where r=6cm, h=30cm and π=3.14
This equals to
2π*6(6+30)
12*3.14*36
1356.48cm2
CLASS3
:THURSDAY23/07/2020
1) Calculate the curved surface area of a cylinder whose radius is
14cm and whose height is 20cm
SOLUTION
The curved surface area of a cylinder is given by 2πrh
Where radius =14cm height=20cm
The curved surface area is 2*22/7*14*20
Which is equal to 2*22*2*20
1760cm2
QUESTION2
2) A cylindrical water tank is closed at both ends>if the radius of the
tank is 0.5m and the height is 0.75m, find the total surface area of the
tank to the nearest square meters..(take π=3.142)
SOLUTION
Total surface area of a cylindrical tanks closed at both ends is
Total
surface area of a closed cylinder is
given as
2πr2+2πrh
This can be simplified as
2πr(r+h)
Where r= 0.5cm,h=0.75cm
This gives us
2π*0.5(0.5+0.75)
This equals
1.0*π*1.25
With π=3.142
1*3.142*1.25
This equals
3.9275
QUESTION3
3) The circumference of the base of a solid cylinder is 88cm. If the
height is 9cm, find the curved surface area.(take π=22/7)
Circumference of a circle is given as
Πd or 2πr
Where d=diameter and r=radius
2πr=88
Therefore
r=88/(2π)
where π=22/7
r=88/(2*22/7)
on simplifying we have
r=44(22/7)
on further simplification we have
r=2*(1/7)
r=2*7
this gives
r=14cm
curved surface area of a solid cylinder is given as
The curved surface area of a cylinder is given by 2πrh
Where r=14cm, h=9cm
This gives us
2*(22/7)*14*9
This equals 792cm2
CLASS 1: TUESDAY 14/07/2020
1) Calculate the curved surface area of a cylindrical container with these
dimensions:
(Take π=3.142)
Diameter 20cm, length 32cm
2) Diameter 52cm, height 42cm.
3)Take π to be 22/7 to find the total surface area of a closed cylinder of radius 7cm and height 30cm.
CLASS2: WEDNESDAY 15/07/2020
- A closed tin is in the shape of a cylinder of diameter 42cm and height
300cm.Use the value of 22/7 for π to find the curved surface area of the tin - A cylindrical cup has a circular base of radius 35 cm and height
of 20cm.Taking the value of π to be 22/7 calculate:
a) total surface area
b) the area of its circular base
- A cylinder is of height 30cm and base radius 6cm.Use the value 3.14 for to
calculate the total surface to the nearest cm2
CLASS 3:THURSDAY 16/07/2020
1)Calculate the curved surface area of a cylinder whose radius is 14cm and whose height is 20cm
2) A cylindrical water tank is closed at both ends>if the radius of the tank is 0.5m and the height is 0.75m, find the total surface area of the tank to the nearest square meters..
3) The circumference of the base of a solid cylinder is 88cm. If the height is 9cm, find the curved surface area.
4)The length of a cylindrical pipe which is 2cm thick is 120cm and its diameter is 12cm;
a) Find the surface area of the inner curve to one decimal place
b)find the diameter of the hole.
CLASS1:TUESDAY 07/07/2020
CORECTION OF LAST ASSIGNMENT
1) Calculate the curved surface area of a cylindrical container with these
dimensions:
(Take π=3.142)
Diameter 10cm, length 18cm
2) Diameter 58cm, height 86cm
3 Take π to be 22/7 to find the total surface area of a
closed cylinder of radius 7cm and height 30cm
SOLUTION TO QUESTION 1
Curved area of cylinder is given as 2 π rh
Where h= height
=18cm,
R=diameter/2=10/2=5cm
Curved surface area
is given as 2*3.142*18*5=565.56cm2
SOLUTION TO QUESTION 2
Curved area of cylinder is given as 2 π rh
Where h= height =86cm, r=diameter/2=58/2=29cm
Curved surface
area is given as
2*3.142*29*86=15672.296cm2
SOLUTION TO QUESTION 3
3) Take P to be 22/7 to find the
total surface area of a closed cylinder of radius 7cm and height 30cm
Total surface area of a closed cylinder is given as
2πr2 +2π rh
This can
be simplified as
2
π hr(r+h)
Where r=7cm , h=30cm
2P*7*30(7+30)
2*(22/7)*7*30(37)
This can be simplified as
2*22*30*37=48840cm2
CLASS2:WEDNESDAY 08/07/2020
SOLUTION TO QUESTION 1
1) A cylinder is of height 5cm and base radius 2cm.Use the value 3.14 for to
calculate the area of its curved surface to the nearest cm2 .
1)Curved surface area is given as
2Prh
Where r=2cm , h=5cm and P=3.14
2*3.14*2*5=62.8cm2
SOLUTION TO QUESTION 2
2) A closed tin is in the shape of a cylinder of diameter 21cm and height
10cm.Use the value of 22/7 for π to find the total surface area of the tin
total surface area is given as
2πr2 +2 π rh
This can be simplified as
2π hr(r+h)
Where r=diameter/2=21/2=10.5cm
h=height=10cm
this gives us
2*22/7*10*10.5(10.5+10)
44/7*10*10.5(20.5)
44*10*1.5(20.5)
=13530cm2
SOLUTION TO QUESTION 3
3) 3)A cylindrical cup has a circular base of radius 14cm and height
of 20cm.Taking the value of π to be 22/7 calculate:
a)Its curved surface
b) the area of its circular base
curved surface area is given as
2 πrh
This is given as
2*22/7*14*20
This equals
2*22*2*20
1760cm2
b)the area of its base is given as
πr2
where r=14cm,
this gives us
22/7*14
This equals
22*2=44cm2
3) Calculate the curved surface area of cylinder of radius 6cm and height
15cm. (Take π =3.142)
curved surface area is given as
2 πrh
This is given as
2*3.142*6*15=
565.56cm2
THURSDAY 09/07/2020
SOLUTION TO QUESTION 1
1)A student winds a strip of paper eight times round a cylindrical
pencil of diameter of 7mm. Use the value of 22/7 for to find the
length of the paper (ignore the thickness of the paper)
Area of the circular base equals total length of the paper=
π r2
Where π=22/7 and r=7mm
(22/7)*7
This equals
22cm2
It was wound 8 times
The total length =8*22=176cm2
SOLUTION TO QUESTION 2
2) A newspaper is rolled into a cylindrical shape of approximate diameter
4cm. It is wrapped for posting with a strip of paper which goes 2 times round
the paper . Use the value of 3 for π to
find the approximate length of the wrapping paper.
Area of the circular base equals total length of the paper=
Πr2
Where π=3 and r=diameter/2=4/2=2cm
3*22
3*4
12cm2
SOLUTION TO QUESTION 3
3) Calculate the curved surface area of cylinder of radius 6cm and height
15cm. (Take π =3.142)
Solution
the curved surface area of cylinder= 2πrh
2*3.142*6*15=
565.56cm2
CLASS 1: TUESDAY 30/06/2020
1) Calculate the curved surface area of a cylindrical container with these dimensions
(Take π=3.142 ):
Diameter 10cm, length 18cm
2) Diameter 58cm, height 86cm
3 Take be 22/7 to find the surface area of a closed cylinder of radius 7cm and height 30cm
CLASS 2: WEDNESDAY 01/07/2020
1) A cylinder is of height 5cm and base radius 2cm.Use the value 3.14 for to calculate the area of its curved surface to the nearest cm2 .
2) A closed tin is in the shape of a cylinder of diameter 21cm and height 10cm.Use the value of 22/7 for π to find the total surface area of the tin
3)A cylindrical cup has a circular base of radius 14cm and height of 20cm.Taking the value of π to be 22/7 calculate:
a)Its curved surface
b) the area of its circular base
4)Calculate the surface area of cylinder of radius 18cm and height 30cm(Take
π
=3.14)
CLASS 3: THURSDAY 02/07/2020
1)A student winds a strip of paper eight times round a cylindrical pencil of diameter of 7mm. Use the value of 22/7 for to find the length of the paper (ignore the thickness of the paper)
2) A newspaper is rolled into a cylindrical shape of approximate diameter 4cm. It is wrapped for posting with a strip of paper which goes 2 times round the paper . Use the value of3 for to find the approximate length of the wrapping paper.
3) Calculate the curved surface area of cylinder of radius 6cm and height 15cm. (Take π =3.142)
CLASS 1:TUESDAY 23/06/2020
CYLINDERS AND CONES
Surface Area of Cylinder
The surface of a cylinder is in three parts: two circular faces and one curved surface
The net of a cylinder is the plane shape you get if you open out a hollow cylinder.
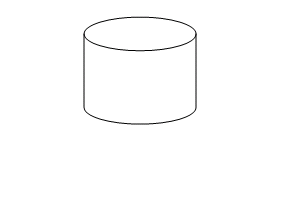
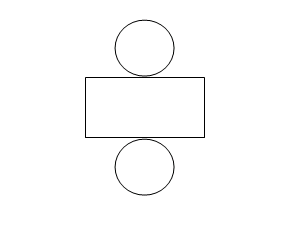
Formular for Surface Area of A Cylinder
Consider a cylinder of height h which has circular faces of radius r
Area of the two cicular faces =∏r2 +∏r2
=2∏r2
The Curved surface is equivalent to a plane rectangle.
Length of rectangle = Circumference of circular face
=2∏r
Breadth of rectangle=h
Area of rectangle =2∏rh
Thus, area of curved surface=2∏rh
Total surface area of closed cylinder=2∏r2+2∏rh
CLASS 2 : WEDNESDAY 24/06/2020
Example1
Calculate the curved surface area of a closed cylindrical container with radius 30cm, height 36cm
(take ∏ to be 3.147)
Solution
Formular for curved surface =2∏rh
Where h=36cm r=30cm
Therefore curved surface area =2*3.142*30*36
=6789.72cm2
Example 2
A closed tin is in shape of a cylinder of diameter 14cm and height 15cm .Use the value of ∏=22/7 find the total surface area of the tin.
Total surface area of a close area is given as 2∏r2+2∏rh
Where r=diameter/2=14/2 =7 h=height=15cm
Solution
The formular can be simplified as 2∏r(r+h)
2∏*7(7+15)
14∏(22)
This gives us
14*22/7(22)
This simplifies as
2*22*22
This equals to
968cm2
CLASS 3: THURSDAY 25/06/2020
EXAMPLE 1
Calculate the curved surface area of cylinder with radius 10cm and height 7cm.(take ∏ =22/7)
Solution
Curved surface area of a cylinder is given as 2∏rh
With r=10cm, height=7cm
2*22/7*(10*7)
44/7(70)
This equals to
=440cm2
EXAMPLE 2
Usethe value 22/7 for ∏ to find the total surface area of a closed cylinder of height 20cm and radius 28cm
Solution
Total surface area of a closed cylinder is given as 2∏r2+2∏rh
This is simplified as 2∏r(r+h)
Where h=20cm and r=28cm
2*(22/7)*28(28+20)
44*28/7(48)
This is simplified as
44*4*48=
8448cm2
CORRECTION OF LAST WEEK ASSIGNMENT
CLASS 1:TUESDAY 16/06/2020
Find out which of these are Pythagorean triples
(24, 58, 62)
b) (14, 49, 50)
C) (15, 36, 39)
(24,58, 62)
b) (14, 49, 50)
C) (15, 36, 39)
SOLUTION
Find out which of these are Pythagorean triples
(24, 58, 62)
b) (14, 49, 50)
C) (15, 36, 39)
(24,
58, 62)
b) (14, 49, 50)
C) (15, 36, 39)
SOLUTION
1a)242=24*24=576
582=58*58=3364
622=62*62=3844
576+3363=3940.
This is not equal to 3844. Therefore (24, 58, 62)
is not Pythagorean triple
1b)
142=14*14=196
492=49*49=2401
502=50*50=2500
196+2401=2597
This is not equal to 2501.Therefore) (14, 49, 50) is not Pythagorean triple.
1C) (15, 36, 39)
152=15*15=225
362=36*36=1296
392=39*39=1521
225+1296=1521
Since
225+1296=392
Therefore
(15, 36, 39) is a Pythagorean triple.
2) Calculate to 2s.f the length of diagonal of a square that measures 20cm by 20cm
Diagonals
of square meet to form a right angle triangle
Given a square ABCD with diagonals BD and AC
AB2=DC2+BC2
With AD=BC =20CM
AB2=202+202
=400 +400=800
AB=√800
AB=
3)A student cycles from home to school first eastwards to a road junction 12km
from home, then southwards to school. If the school is 19km from home. How far
is it from the road junction?

![]()
![]() A 12
A 12
B
19 X
C
AC2=AB2+BC2
192=122+BC2
361=144+BC
361-144=BC2
BC2=217
BC=√217
BC=14.73
CLASS 2 WEDNESDAY17/06/2020
Which of these are Pythagoreans
triple?
a)(10,24,26)
b)(12,29.32)
c)(14,49,50)
SOLUTION
1a)
102=10*10=100
242=24*24=576
262=26*26=676
100+576=676=262
Therefore (10, 24, 26) is Pythagorean triple
1b) (12, 29, 32)
122=12*12=144
292=29*29=841
322=32*32=1024
144+841=985
This is not equal to 1024
(12, 29, 32) is not Pythagoreans triple.
c) (14, 49, 50)
142=14*14=196
492=49*49=2401
502=50*50=2500
196+2401=2597
This is not equal to 2500
Therefore (14, 49, 50) is not a Pythagorean
triple.
2)
A rectangle measures 8cm by 15cm. Use Pythagoreans rule to calculate the length
of one of its diagonals.
Given
a rectangle ABCD with AC and BD as diagonals right angle at D and C
AC2=AD2+DC2
AC2=82+152
=64+225
=289
AC=√289
AC=17.

![]() 3) A ladder 9.6m long leans against a wall. It
3) A ladder 9.6m long leans against a wall. It
touches the wall at a point 9m above the ground .Find the distance of the foot
of the ladder from the wall.
C
9.6M 9M
![]()
A XCM B
The ladder forms a right angle triangle at B
AC2=AB2+BC2
9.62=AB2 +92
92.16-81=AB2
AB2=11.16
AB=√11.16
AB=3.34
CLASS 3 THURSDAY 18/06/2020
1) Which of these are Pythagoreans triples?
a) (3, 4, 5)
b) (5, 12, 13)
(8, 13, 17)
SOLUTION
1a)
(3, 4,5)
32=3*3=9
42=4*4=16
52=5*5=25
9+16=25=52
(3,4,5) is a Pythagoreans triple
b)(5,12,13)
52=5*5=25
122=12*12=144
132=13*13=169
25+144=169=132
(5,
12, 13) is a Pythagoreans triple
1c) (8,13,17)
82=8*8=64
132=13*13=169
172=17*17=289
64+169=233
233 is not equal to 172 .
2) PQRS is a rectangle with sides 3cm and 4cm.If its diagonals cross at o calculate the
length po
 |
3
4
The diagonal of the rectangle and other sides form a right angle triangle. Then
with PR and QS are diagonal of the triangle. Then we have,
QS2=32+42
QS2=
9+16=25
QS=√25
QS=5
DATE POSTED:MONDAY 08/06/2020
CLASS 1:TUESDAY 09/02/2020
Find out which of these are pythagorean triples
(24,58,62)
b) (14,49,50)
C)(15,36,39)
2)Calculate to 2s.f the length of a diagonal of a square that measures 20cm by 20cm
3) A student cycles from home to school first eastwards to a road junction 12km from home,then southwards to school.if the school is 19km from home. How far is it from the road junction,
CLASS 2:DATE WEDNESDAY 10/06/2020
Which of these are pythagoreans triple?
a)(10,24,26)
b)(12,29.32)
c)(14,49,50)
2)A rectangle measures 8cm by 15cm. Use pythagoreans rule to calculate the length of one of its diagonals.
3)A ladder 9.6m long leans against a wall.it touches the wall at a point 9m above the ground .Find the distance of the foot of the ladder from the wall.
CLASS 3 THURSDAY 11/06/2020
1)Which of these are Pythagoreans triples?
a)(3,4,5)
b)(5,12,13)
(8,13,17)
2)PQRS is a rectangle with sides 3cm and 4cm.If its diagonals cross at o calculate the length po
3) The diagonals of a rhombus measure 8cm by 6cm.What is the length of a side of the rhombus?
DATE POSTED 02/06/2020
CORRECTION OF LAST WEEK ASSIGNMENT
Thursday 28/05/2020
1) Solve
3(2X-1)/4=4(X+2)/3-3
Solution
Multiply LHS and RHS by the lcm of 12
12*3(2X-1)/4=12*4(X+2)/3-12*3
This is simplified to give,
3*3(2X-1)=4*4(X+2)-36
This gives us,
9(2X-1)=16(X+2)-36
Opening the bracket we have,
18X-9=16X+32-36
18X-9=16X-4,
Collecting like terms,
18X-16X=-4+9,
This gives us,
2X=5
Divide both sides by 2,
2X/2=5/2
This gives,
X=2.5
2)Let the number be Y
Subtract 17 from the number gives us,
Y-17
Divide the result by 5 we have,
(Y-17)/5
The final answer is 3,
This gives us,
(Y-17)/5=3,
On cross multiplication,
(Y-17)=3*5
(Y-17)=15
Collecting like terms
Y=15+17
Y=32
3)Let the number be Z
Subtract 14 from the number gives,
Z-14,
With the difference trebled,
3(Z-14),………………………………………(1)
Two third of the number is
(2/3)Z………………………………………………(2)
The result in (1) is equal to (2)
3(Z-14)=(2/3)Z
Multiply both sides by LCM of 3,
3*3(Z-14)=3*(2/3)Z,
This is simplified to give
9(Z-14)=2Z
Opening the bracket we have,
9Z-126=2Z
Collecting like terms,
9Z-2Z=126
7Z=126
Divide both sides by 7,
7Z/7=126/7
This gives ,
Z=18
DATE WEDNESDAY 27/05/2020
WORD PROBLEMS INVOLVING SOLVING EQUATIONS
A number is multiplied by 6 and then 4 is added. The result is 34, find the number.
Solution
Let the number be X.
The number multiplied by X gives
6*X=6X……………………..(1)
Addition of 4 to (1) gives
6X+4…………………………(2)
The result of (2) gives 34
Then we have
6X+4=34…………………..(3)
Subtract 4 from both sides of the equations
6X+4-4=34-4
This gives
6X=30
Divide both equations by 6
6X/6=30/6
This gives
X=5
Example 2
I am thinking of a number. I take away 5.The result is 14.Wnat number did I think of?
Solution
Let the number be Y.
Taking away 5 from the number gives
Y-5……………………….(1)
The result of (1) is 14
Y-5=14
Add 5 to both sides of the equations
Y-5+5=14+5
This gives
Y=19
ASSIGNMENT
- I think of a number .I double it the result is 96. Find the number.
- When I add a number to another number four times as big, the result is 30.Find the number.
- I add 12 to a certain number and then double the result. The answer is 42. Find the original number
- I subtract 8 from a certain number. I then multiply the result by 3. The final answer is 21. Find the original number
DATE: THURSDAY 25/05/2020
WORD PROBLEMS INVOLVING SOLVING EQUATIONS 2
Example1
I think of a number .I double it .I divide the result by 5.My answer is 6 .What number did I think of?
Solution
Let the number be M
Doubling the number gives
2*M=2M…………………….(1)
Dividing (1) by 5 gives
2M/5
The answer is 6
2M/5=6
Cross multiply
2M=6*5
2M=30…………………(2)
Divide by (2)
2M/2=30/2
M=15
Example 2
I add 45 to a certain number and then divide the sum by 2. The result is 5 times the original number. Find the number.
Solution
Let the number be Z
Addition of 45 to Z gives
45+Z……………………………(1)
Divide (1) by 2 gives
(45+Z)/2………………………(2)
Five times the original number gives
5Z
The result (1) IS equal to (2)
(45+Z)/2=5Z
Cross multiply
45+Z=2*5Z
This gives
45+Z=10Z
Subtract Z from both sides of the equations
45+Z-Z=10Z-Z
This gives
45=9Z
Divide both sides by 9
45/9=9Z/9
This gives
Z=5
ASSIGNMENT
Solve these equations
1)b+3/5=3b+3/3
2)3(2x-1)/4=4(x+2)/3-3
3)i subtract 17 from a certain number and then divide the result by 5.My final answer is 3. What was the original number?
4) I think of a number. I subtract 14 from the number and then treble the difference .The result is two-thirds of the number. Find the original number
Correction to last assignment
Wednesday 27/05/2020
Let the number be X
When the number is double that gives 2*X
If the result is 96,
That gives us,
2X=96
Divide both sides by 2,
2X/2=96/2
X=48
2)Let the number be Z
Four times the number=4*X
Addition of the number with 4 times the number equals
X +4X
The result is 20
This gives us
X+4X=20 ,
5X=20
Divide both sides by 5
5X/5=20/5
X=4
3)Let the number be Y
Addition of 12 to the number gives
Y+12
Doubling the result gives
(Y+12)2
The answer is 42
2(Y+12)=42
Opening the bracket
2Y+24=42
Collect like terms,
2Y=42-24
2Y=18
Divide both sides by 2,
2Y/2=18/2
Y=9
4)Let the number be M
Subtract 8 from the number gives
M-8
Multiply the result by 3
(M-8)*3
The final answer is 21
This gives us
3(M-8)=21
Opening brackets.
3M-24=21
Collect like terms
3M=21+24
This gives
3M=45
Divide both sides by 3
3M/3=45/3
M=15
DATE POSTED TUESDAY 02/06/2020
LESSON 1
Tesday 2/06/2020
PYTHAGORAS RULE
Pythagoras Rule shows the relationship between hypotenuse adjacent and opposite in a right angle triangle.
Example 1
Given any right angle-angled triangle with hypotenuse c and any other sides a and b;
C2=a2+b2
Calculate the value of side c
C 3
4
Using Pythagoras rule,
C2=32 +42
C2=9+16
c=√25
C=5
Example2
Using Pythagoras rule calculate the length of the third side of the triangle
10 a
8
102=a2+82
100=a2+64
100-64=a
a2=√36
a=6
ASSIGNMENT
ABC is a triangle in which angle B =90 .In each of these draw and labeled a sketch and then calculate the length of the third side
1)AB=15cm, BC=8cm
2)AC=25cm, BC=20cm
3)AC=26cm, AB=24cm
4)AC=100cm, AB=24 cm
LESSON 2
DATE Wednesday 3/06/2020
Pythagorean Triples
A Pythagorean triple is a set of three whole numbers which give the lengths of the sides of right-angled triangles e.g(5,12,13), (7,24,25) (8,15,17) are common Pythagoreans triple
Example1
Which of these is a Pythagoreans triple?
(33,56,65)
Solution
a)332 +562=1089+3136
=4225
652=4225
Thus 332+562=652
Example2
(15,30,35)
152+302=225 +900
1125
352=1225
Thus 152+302=352
ASSIGNMENT
Find out which of these are Pythagoreans triple
- (20,21,29)
- (20,22,26)
- (30,40,50)
- (14,24,28)
LESSON 3
DATE Thursday 4/06/2020
CLASSWORK
!)Find the length of the longest straight line which can be drawn on arectangular chalkboard which measures 2.2m by 1.2m
2)A plane flies northward for 430km.It then flies eastward for 380km. How far is it from its starting point.
3)The distance between the opposite corners of a rectangular plot is 30m .The length of the plot is 24m.Calculate the breadth of the plot.
DATE POSTED 02/06/2020
CORRECTION OF LAST WEEK ASSIGNMENT
Thursday 28/05/2020
1) Solve
3(2X-1)/4=4(X+2)/3-3
Solution
Multiply LHS and RHS by the lcm of 12
12*3(2X-1)/4=12*4(X+2)/3-12*3
This is simplified to give,
3*3(2X-1)=4*4(X+2)-36
This gives us,
9(2X-1)=16(X+2)-36
Opening the bracket we have,
18X-9=16X+32-36
18X-9=16X-4,
Collecting like terms,
18X-16X=-4+9,
This gives us,
2X=5
Divide both sides by 2,
2X/2=5/2
This gives,
X=2.5
2)Let the number be Y
Subtract 17 from the number gives us,
Y-17
Divide the result by 5 we have,
(Y-17)/5
The final answer is 3,
This gives us,
(Y-17)/5=3,
On cross multiplication,
(Y-17)=3*5
(Y-17)=15
Collecting like terms
Y=15+17
Y=32
3)Let the number be Z
Subtract 14 from the number gives,
Z-14,
With the difference trebled,
3(Z-14),………………………………………(1)
Two third of the number is
(2/3)Z………………………………………………(2)
The result in (1) is equal to (2)
3(Z-14)=(2/3)Z
Multiply both sides by LCM of 3,
3*3(Z-14)=3*(2/3)Z,
This is simplified to give
9(Z-14)=2Z
Opening the bracket we have,
9Z-126=2Z
Collecting like terms,
9Z-2Z=126
7Z=126
Divide both sides by 7,
7Z/7=126/7
This gives ,
Z=18
DATE:26 – 05 20
1.The angles of a quadrilateral are a, 2a,3a+20 and 4a + 30.Find each angle if the sum of the angles of a quadrilateral is 360 degrees.
2.The largest of three consecutive even numbers is n+10.If the sum of these numbers is 66.What are the numbers?
3.The sum of three consecutive even numbers is 60.Find the numbers.
4.The sides of a rectangular field are 3(x+2)m and 2(x+2)m long, respectively.If the perimeter is 90m.Find the length of each side.
5. Think of a number,add 5,the result is 10.What is the number?
6. A couple is blessed with a boy and a girl.The boy’s age is twice that of the girl.In four year’s time .the sum of their ages will be 29 years.What is the age of the boy?
7.The base of a triangle is (x-2)cm,the first sloping side is twice the base in length and the second sloping side is 3 times the length of the base.Find the length of each side of the triangle if the perimeter is 90cm.
THIRD TERM SCHEME OF WORK
Pythagoras’ rule
Right-angle triangles
Pythagoras’ rule
Pythagoras in real life
Statistics 2:
Tables, charts, schedules
Reading tabulated data
Timetables and chart
Cylinders and cones
Cylinders
Cones
Mensuration and estimation
Angles2: Elevation and depression
Horizontal and vertical
Elevation and depression
Scale drawings
Statistics 3: Probability
Experimental probability
Probability as a fraction
Linear inequalities
Inequalities
Graphs of inequalities
Solution of inequalities
Graphs 3:
Graphs of linear equations
Linear equations and graphs
Properties of linear graphs
Bearing and distances
Compass directions
Bearings
Bearing and distances
Bearing and distances
WEEK 2
We are going to start off our revision from last term work from the topic solving equations
Solving Equations
What do we mean by solving equations
To solve an equation means to find the value of the unknown that makes the equation true.
Method 1
Using Directed Numbers method
Example 1
Given an equation of the form
2x-9=15
- x is the unknown in the equation
- 2x-9 is on the left hand side(LHS) of the equals sign
- 15 is on the right hand side of the equations
- Solutions
Add 9 to both sides of the equations.
2x-9+9=15+9
This gives us
2x=24
Divide both sides by 2.
This gives us
2x/2=24/2
x=12
Unknown on both sides of the equations
If an equation has unknown terms on both sides of the equal sign, collect the unknown terms on one side and the number terms on the other side
Example 2
5x+6=2x+21
subtract 2x from both sides of the equations
5x-2x+6=2x-2x+21
This gives
3x+6=21
subtract 6 from both sides of the equations
3x+6-6=21-6
This gives
3x=15
Divide both sides by 3 we have
3x/3=15/3
this gives
x=5
CLASSWORK
Solve these equations
- 4b+24=0
- 7=9-3m
- 11+9n=6n+13
- x+7=19+2x
- 6x+1=26-2x
- 18-5f=2f+4
- 10q=3q-7
- 3x=18-3x
- 4h-2=h+7
- 9x+1=7x
Kindly fill in full name,email,subject name, topic and your answer in the form below.
20-05-20
ASSIGNMENT
8x-14=x-7.
2+x-5=-2x
4x+6=-3x-8
-9x+5=7-8x
x-10+3x=-2x+20
-13-2x=-5x-1
5y-10-3y=2y+20-y
11a-13=9a+3
-7x+13=-8-4x
6d+3=2d+23.
8x-14=x-7.
2+x-5=-2x
4x+6=-3x-8
-9x+5=7-8x
x-10+3x=-2x+20
-13-2x=-5x-1
5y-10-3y=2y+20-y
11a-13=9a+3
-7x+13=-8-4x
6d+3=2d+23.
Correction of last week Assignment
1)8x-14=x-7
collect like terms
8x-x=-7+14
This gives
7x=7
Divide both sides by 7
7x/7=7/7
this gives,
x=1
2)2+x-5=-2x
Collect like terms,
2-5=-2x-x
this gives us,
-3=-3x
divide both sides by -3,
-3/-3=-3x/-3
then we have,
1=x or
x=1
3)4x+6=-3x-8
collect like terms,
4x+3x=-8-6
this gives us,
7x=-14
divide both sides by 7 we have,
7x/7=-14/7
This gives us,
x=-2
3)4x +6=-3x-8
Collect like terms
4x+3x=-8-6
This gives us,
7x=-14
Divide both sides by 7,
7x/7=-14/7
X=-2
4) -9x+5=7-8x
Collect like terms,
-9x+8x=7-5
-x=2
Multiply both sides by -1 this gives us,
X=-2
5) x-10+3x=-2x+20
Collect like terms,
X+3x+2x=20+10
This gives us
6x=30
Divide both sides by 6,
6x/6=30/6
This gives us,
X=5
6) -13-2x=-5x-1
Collect like terms
-13+1=-5x+2x
-12=-3x
Divide both sides by -3,
-12/-3=-3x/-3
4=x
Or
X=4
7) 5y-10-3y=2y+20-y
Collect like terms,
5y-3y-2y+y=20+10
Y=30
8) 11a-13=9a+3
Collect like terms ,
11a-9a=3+13
This gives us,
2a=16
Divide both sides by 2 we have,
2a/2=16/2
a=8
9) -7x+13=-8-4x
Collect like terms,
-7x+4x=-8-13
-3x=-21
Divide both sides by -3 we have,
-3x/-3=-21/-3
This gives us
X=7
10) 6d+3=2d+23.
Collect like terms we have,
6d-2d=23-3
This gives us
4d=20,
Divide both sides by 4,
4d/4=20/4
d= 5
DATE WEDNESDAY 27/05/2020
WORD PROBLEMS INVOLVING SOLVING EQUATIONS
A number is multiplied by 6 and then 4 is added. The result is 34, find the number.
Solution
Let the number be X.
The number multiplied by X gives
6*X=6X……………………..(1)
Addition of 4 to (1) gives
6X+4…………………………(2)
The result of (2) gives 34
Then we have
6X+4=34…………………..(3)
Subtract 4 from both sides of the equations
6X+4-4=34-4
This gives
6X=30
Divide both equations by 6
6Xx/6=30/6
This gives
X=5
Example 2
I am thinking of a number. I take away 5.The result is 14.Wnat number did I think of?
Solution
Let the number be Y.
Taking away 5 from the number gives
Y-5……………………….(1)
The result of (1) is 14
Y-5=14
Add 5 to both sides of the equations
Y-5+5=14+5
This gives
Y=19
ASSIGNMENT
- I think of a number .I double it the result is 96. Find the number.
- When I add a number to another number four times as big, the result is 30.Find the number.
- I add 12 to a certain number and then double the result. The answer is 42. Find the original number
- I subtract 8 from a certain number. I then multiply the result by 3. The final answer is 21. Find the original number
DATE: THURSDAY 25/05/2020
WORD PROBLEMS INVOLVING SOLVING EQUATIONS 2
Example1
I think of a number .I double it .I divide the result by 5.My answer is 6 .What number did I think of?
Solution
Let the number be M
Doubling the number gives
2*M=2M…………………….(1)
Dividing (1) by 5 gives
2M/5
The answer is 6
2M/5=6
Cross multiply
2M=6*5
2M=30…………………(2)
Divide (2)
2M/2=30/2
M=15
Example 2
I add 45 to a certain number and then divide the sum by 2. The result is 5 times the original number. Find the number.
Solution
Let the number be Z
Addition of 45 to Z gives
45+Z……………………………(1)
Divide (1) by 2 gives
45+Z/2………………………(2)
Five times the original number gives
5Z
The result (1) IS equal to (2)
45+Z/2=5Z
Cross multiply
45+Z=2*5Z
This gives
45+Z=10Z
Subtract Z from both sides of the equations
45+Z-Z=10Z-Z
This gives
45=9Z
Divide both sides by 9
45/9=9Z/9
This gives
Z=5
ASSIGNMENT
Solve these equations
1)b+3/5=3b+3/3
2)3(2x-1)/4=4(x+2)/3-3
3)i subtract 17 from a certain number and then divide the result by 5.My final answer is 3. What was the original number?
4) I think of a number. I subtract 14 from the number and then treble the difference .The result is two-thirds of the number. Find the original number
Correction of last week Assignment
Wednesday 27/05/2020
1)Let the number be X
When the number is doubled we have,
2*X=2X
The result is 96
That means
2X=96,
Divide both sides by 2,
2X/2=96/2
That gives us
X=48
2)Let the number be Y
Four times as big is
4*Y=4Y
Addition of the number with four times as big is,
Y+4Y,
The result is 30,
Y+4Y=30
This gives us,
5Y=30
Divide both sides by 5,
5Y/5=30/5
This gives
Y=6
3)Let the number be Z
Addition of 12 to the number gives,
12+Z=Z+12
The result is doubled gives,
2(Z+12)
The answer is 42 equals,
2(Z+12)=42
Opening the bracket
2Z+24=42,
Collect like terms gives us,
2Z=42-24,
This gives us,
2Z=18
Divide both sides by 2,
2Z/2=18/2
That means,
Z=9
4)Let the number be M
When 8 is subtracted from the number gives us,
M-8,
When the result is multiplied by 3,
That gives us,
3(M-8),
The final answer is 21,
This gives us,
3(M-8)=21
Opening the bracket,
3M-24=21,
Collect like terms we have,
3M=21+24
That gives us,
3M=45,
Divide both sides by 3 we have,
3M/3=45/3
M=15